¿Cómo se llamaba el gato de Schrödinger?


Mirad que camisetas más chulas:
Noticias, curiosidades, artículos propios y ajenos, simulaciones, libros, literatura, arte, reflexiones, atajos para resolver problemas, anécdotas ... relacionadas sobre todo con la Física en todo su esplendor: cuántica, estado sólido, cosmología, astrofísica, matemáticas, ciencia ficción y un largo etc.


Mirad que camisetas más chulas:
Publicado por
Unknown
el
jueves, octubre 26, 2006
7
comentarios
![]()
Vuelve la semana de la ciencia, con charlas, cursos, exposiciones, jornadas de puertas abiertas, etc.
El enlace principal está en: Semana de la Ciencia
Recomiendo varias actividades, como por ejemplo, el ciclo de conferencias de matemáticas, en la Univerisdad Autónoma. Hay algunas interesantes en la complutense. Por ejemplo hay un taller sobre Criptografía, otra sobre cristales líquidos, ciclo de jornadas astronomícas, ... podeis verlo en el enlace de actividades en la Complutense
Puede ser interesante llevar a los niños al pasaparques científico. Los Científicos Locos de "Mad Science" echarán sus artilugios a la mochila para presentar, en algunos de los parques más emblemáticos de Madrid, el primer y más original "Pasaparques Científico" que hayas visto (según dicen ellos).
Será los días:
9 y 12. Parque Juan Carlos I - Zona entrada Campo de las Naciones
12 y 19. Parque del Retiro - Zona del Estanque
9 y 19. Parque del Oeste - Zona del Templo de Debod, Parque Juan Carlos I
Publicado por
Unknown
el
miércoles, octubre 25, 2006
0
comentarios
![]()
Etiquetas: Eventos, Física General, Matemáticas, Noticias
Por razones varias, que tienen que ver sobre todo con la gran pregunta: ¿qué cojones hago trabajando en esto? (y no con la gran respuesta: 42), necesito recordarme de vez en cuando porqué empecé a estudiar física. Así que continuo esta línea de búsqueda de la belleza en la ciencia, y adjunto un par de imágenes espectaculares.
Simulación del patrón del flujo de electrones viajando en un paisaje a nanoescala, atrapados en la interfase entre dos solidos.
Funciones de Bessel. Resultado de la superposición de 21 ondas planas.
Otras imágenes. Por cierto, se venden posters.
Por supuesto, no puedo dejar fuera las imágenes que tanto me atrajeron desde pequeñito:
El resto de Escher
Publicado por
Unknown
el
martes, octubre 24, 2006
0
comentarios
![]()
Etiquetas: Belleza, Física Teórica, Imágenes
Todos conocemos el aspecto que tienen los copos de nieve: esas preciosas estructuras cuasi-fractales con simetría hexagonal. Pero nunca había visto una micrografía tan cercana de un copo de nieve. Realmente es fascinante (fijaos en la escala de cada figura).

Publicado por
Mario Castro
el
lunes, octubre 23, 2006
0
comentarios
![]()
Etiquetas: Belleza, Física General, Imágenes, Órden de Magnitud
Se ha puesto a disposición del público la obra completa de Charles Darwin.
Los libros están escaneados y, no sólo eso, sino que se ha escaneado también el cuaderno de notas que llevaba en el Beagle o la primera edición de El origen de las especies (libro que os recomiendo encarecidamente. Es algo denso en algunos pasajes, pero tiene permite vislumbrar el genio de Darwin).
Esto supongo que es un adelanto de la paliza que nos van a dar en 2009 cuando se celebre el bicentenario de su nacimiento, en 2009
Publicado por
Mario Castro
el
viernes, octubre 20, 2006
0
comentarios
![]()
Hace poco puse un fotografía de la nebulosa de la Antena, en que se apreciaba el choque entre dos galaxias. Ahora el Hubble ha hecho fotos a bastante más resolución, por lo que se puede estudiar la creación de nuevas estrellas en ese "choque". Las imágenes son impresionantes, y hay videos con una animación en la que se puede apreciar la resolución necesaria para captar estos detalles.
Sitio original de las imágenes
Animación en formato QuickTime
Animación en formato Mpeg
Alta resolución (40 mb)
Detalle
Publicado por
Unknown
el
jueves, octubre 19, 2006
0
comentarios
![]()
Etiquetas: Astronomía, Belleza, Noticias
Estamos ante un caso de aplicación de redes complejas a un sistema integrado en Internet, en el que se descubre una ley de potencias. ¡Qué bonito!
Se ha estudiado cómo se conecta la gente a un sitio de noticias bastante popular en Internet (250.000 visitas al mes, casi como nuestro Blog). Estudiando las trazas dejadas en el portal, se ha visto que raramente se visita una página más allá de las 36 horas de haberse publicado (vida media de la página)
Albert-László Barabási, de la Universidad de NotreDame ha encontrado que el número de personas que lee noticias en la web decae con el tiempo según una ley de potencias, y no exponencialmente, como se creía.
El esqueleto del portal estudiado tenía 933 nodos. El área del círculo asignado a cada nudo en la figura es proporcional al logaritmo del número total de visitas al documento web correspondiente. El grosor de la línea es proporcional al logaritmo del número total de veces que el enlace fué usado por los usuarios en el portal.
Sería interesante repetir el estudio con blogs y portales de diferentes tipos, no sólo con un portal de noticias. Es evidente que las noticias dejan de tener actualidad rápidamente, por eso en ingles se llaman News, y no Olds. Pero seguro que un sitio con información más valiosa para el conocimiento se comporte de otra manera.
Artículo original
Publicado por
Unknown
el
miércoles, octubre 18, 2006
3
comentarios
![]()
Etiquetas: Noticias
Podeis encontrar una base de datos de exámenes, algunos resueltos, de la carrera de Físicas, en el siguiente enlace
Exámenes
Algunos más, de los primeros cursos, en Exámemes de primer ciclo de Físicas, en la página personal de Jacín.
En la universidad Durham tenéis otro repositorio de exámenes de Física.
Iré añadiendo sitios, según los encentre o me acuerde.
Publicado por
Unknown
el
viernes, octubre 13, 2006
3
comentarios
![]()
Etiquetas: Exámenes y Problemas, Libros
Integramos dos Blog, éste en el que estáis y el de Ciencia, Simulaciones, Linux y otros animales.
Hemos añadido las entradas que tenía el otro blog, y empezaremos a trabajar en paralelo, que cunde más.
Bienvenido, Donlockwood.
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Computación
La Informática es una gran ciencia. En contra de lo que podemos pensar como usuarios, es una disciplina bien estructurada, en ocasiones infinitamente mejor pensada que la arquitectura o la ingeniería civil. Y sin embargo, las casas apenas se caen y los sistemas informáticos apenas se sostienen.
La culpa, desde mi punto de vista, no la tiene la Informática sino el desempeño de la misma. ¿Quién quiere hacer un buen diseño de un software si los 40 días que necesitaría para la documentación y análisis del problema se los doy a los pobres becarios (físicos como yo muchos de ellos) para que programen casi a ciegas?
En otras palabras, la Informática es una ciencia, pero los informáticos (en general y sobre todo muchos intrusos de otros campos) son pobres ingenieros informáticos.
Esta reflexión no tiene mayor transcendencia (salvo la de una conversación en un bar) si no fuera por el decisivo papel que puede tener la informática en otras ciencias. Muchos físicos como yo dependemos de la misma para desarrollar nuestras teorías, contrastarlas y representar la información en la pantalla de un ordenador.
La cuestión es, ¿podemos aprovecharnos de la teoría que subyace a la Informática para hacer mejor nuestra ciencia? Mi respuesta es sí.
Os pondré un ejemplo (que desarrollaré otro día cuando os hable de mi proyecto de crear una librería para integrar [casi] cualquier problema de la Física basado en ecuaciones diferenciales).
Queremos estudiar un cierto modelo que hemos propuesto analíticamente para explicar el fenómeno F. El modelo consiste en una ecuación en derivadas parciales para el observable H que depende del tiempo "t" y de la posición "x" (n-dimensional). ¿Qué hacemos?
1) Cogemos un programa que hayamos desarrollado para un problema similar (en FORTRAN o C) y lo adaptamos al nuevo problema
2) Creamos un nuevo programa que es bastante mejor que los anteriores porque corrige algunos fallos que tenían estos o simplemente nos resulta más fácil de manipular o entender.
3) Conseguimos que alguien nos haga el programa.
La solución 3) es genial, sólo que a veces las cosas no le salen a nuestro colega y nos cuesta un horror entender su código y poder ayudarle.
La solución 2) es la que adoptamos la mayor parte de las veces, máxime teniendo en cuenta que ya no entendemos los códigos que hicimos para otros problemas similares o simplemente no sabríamos cómo modificarlos fácilmente.
La solución 1) está muy bien, sólo que hay que tocar en "N" sitios para que el código al final nos dé el resultado esperado.
¿Pero realmente qué hacen todos nuestros programas?
1) Empieza el programa principal. Se declaran las variables, los parámetros, algunas funciones o subrutinas auxiliares...
2) Se leen datos de un fichero (o de la línea de comandos) para definir los parámetros del problema. Algunos de estos parámetros son del modelo y otros de la simulación (intervalo de tiempo, precisión, número de promedios, semilla del generador de números aleatorios, ...)
3) Se fija la condición inicial, se crean los ficheros de salida, ...
4) Empieza la "simulación" o integración numérica por el método X y periódicamente guardamos el valor de un observable (la media, la varianza, ...) en un fichero.
5) Se post-procesan los resultados de la simulación y ADIOS CHARLIE.
Los que trabajamos con el numérico hacemos esto infinidad de veces.
Otro ejemplo son las simulaciones de Monte Carlo, o autómatas celulares, o simulaciones basadas en agentes (para problemas sociales o biológicos, ...)
La Informática tiene soluciones más serias para estos problemas. Las llaman Metodologías. En particular hay una que causa furor desde hace años y que no está suficientemente explotada por los científicos de otras áreas (como siempre, hablo en términos generales desde mi reducida perspectiva): la orientación a objetos.
La orientación a objetos trabaja con abstracciones, sin importar los detalles particulares del problema. Así, en el ejemplo que puse antes, lo que importa es que trabajamos con parámetros, campos, números aleatorios, ecuaciones, observables, ...
Bien, definamos objetos para todas estas abstracciones y ya podremos reutilizar de manera transparente y eficiente la mayor parte de nuestro código sin tener que retocar a mano todo el mismo.
Por ejemplo, un código como el que describía anteriormente podría ser así en C++:
#include
main()
{
[...]
fichero >> ParametrosDeLaSimulación;
fichero >> ParametrosDelModelo;
fichero >> ListaDeObservables;
fichero >> Ecuaciones;
algoritmo.set("RungeKutta4");
simulador.crea(Ecuaciones,algoritmo,ParametrosDeLaSimulacion,ParametrosDelModelo,
ListaDeObservables);
simulador.postprocesayguarda(Observables);
}
Esto hay que diseñarlo bien, pero una vez hecho, qué más da que las ecuaciones modelen la erosión de una superficie o el crecimiento de un tumor (cuña publicitaria ;-) ): la estructura es la misma.
En fin, mi conlcusión es:
* Estudiemos Orientación a Objetos
* Hagamos códigos robustos, extensibles, legibles, eficientes y versátiles
* Una vez hecho esto: centrémonos en la ciencia no en la informática.
Otro día hablaré de este último punto, pero lanzo una pregunta ¿no tenéis la impresión de que a veces trabajamos sin un gran proyecto a largo plazo? Es decir, está muy bien el tipo de problemas que estudiamos (si no fuese así tampoco lo admitiríamos) pero, ¿no aspiramos a un conocimiento de mayor nivel? ¿Resolvemos problemas o PROBLEMAS?
En fin, que ya me va entrando hambre.
Esta vez, espero vuestros comentarios.
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Computación
En mi primer post (bueno el segundo) os conté cómo crear una imagen bidimensional a partir de un fichero de datos. En esta entrega os contaré como hacer lo mismo con color.
Para empezar, ya no crearemos un fichero pnm sino uno de tipo ppm. La diferencia reside en que los primeros cuantifican el color con un número entre 0 y 65535 y los segundos con una terna de números entre 0 y 255 que representan la cantidad de rojo verde y azul que contiene la imagen.
Para que entendáis mejor el código voy a crear un código intermedio que hace lo mismo que el del post anterior pero en el nuevo formato.
Así, el código en custión sería
#!/bin/bash
if [ $# -ne 3 ]; then
echo "Sintaxis: $0 Nx Ny fichero_de_entrada "
exit
fi
awk '
BEGIN{max=-100000000; min=100000000;}
{
for (i=1;i<=NF;i=i+1){ if (max<$i) max=$i; if(min>$i) min=$i;}
}
END{print max,min}' $3 | awk -v Nx=$1 -v Ny=$2 '
BEGIN{print "P3\n#\n\n" Nx,Ny "\n255 255 255"}
NR==1 {
max=$1;
min=$2;
}
{
for(i=1;i<=NF;i=i+1) { val=int(($i-min)*255/(max-min)) print val,val,val } }' - $3 >$3.ppm
Fijaos en la diferencias:
1) El tipo de archivo no es "P2" sino "P3".
2) En lugar de incluir una única escala (65535) incluimos tres (255 255 255).
3) Por cada pixel imprimo tres números (con el comando print val, val, val)
¿Qué necesitamos para crear una imagen en color? Pues muy fácil, una paleta. Las paletas permiten hacer una mapping entre un subconjunto de los números reales (entre min y max) a un espacio vectorial de tres dimensiones de enteros (entre 0 y 255).
Existen muchas paletas. Yo he usado una que cree hace siglos para una aplicación en basic que hice en el colegio. La versión awk sería la siguiente:
#!/bin/bash
if [ $# -ne 3 ]; then
echo "Sintaxis: $0 Nx Ny fichero_de_entrada "
exit
fi
awk '
BEGIN{max=-100000000; min=100000000;}
{
for (i=1;i<=NF;i=i+1){if (max<$i) max=$i; if(min>$i) min=$i;}
}
END{print max,min}' $3 | awk -v Nx=$1 -v Ny=$2 '
BEGIN{
for(i=0;i<128;i++) i="0;i<128;i++)" i="0;i<="255;i++)">255) r[i]=255; if(g[i]>255) g[i]=255; if(b[i]>255) b[i]=255;}
print "P3\n#\n\n" Nx,Ny "\n255 255 255"
}
NR==1 {
max=$1;
min=$2;
}
{
for(i=1;i<=NF;i=i+1) { val=int(($i-min)*255/(max-min)) print r[val],g[val],b[val] } }' - $3 >$3.ppm
La definición de la paleta está incluida en los bucles
for(i=0;i<128;i++) i="0;i<128;i++)">
El bucle que aparece a continuación de estas líneas es para comprobar que no hay errores de rango. Si queréis crear otra paleta, sólo teneís que definir las matrices r[], g[] y b[]. MATLAB tienes decenas de paletas definidas que probablemente se puedan exportar. Para que veáis un ejemplo os incluyo una imagen de unas simulaciones de un modelo de Crecimiento de Depósitos de Vapor (CVD). 
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Computación
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Graciosos
Hoy voy a hablar de vim (la versión mejorada de vi). vim tiene todo lo bueno de vi, pero además permite una serie de extensiones, plugins y macros que quitan el aliento. En otra ocasión os hablaré de los plugins y os recomendaré alguno. Mientras podéis disfrutar de todo sobre vim en el enlace
http://www.vim.org
En este post os hablaré del fichero de configuración .vimrc que se encuentra en vuestro directorio $HOME
Este fichero permite incluir una serie parámetros y opciones que se cargan en vim en el momento de arranque.
A continuación os detallo algunas líneas de mi fichero .vimrc que os
pueden ser de utilidad
" Los comentarios van precedidos por unas comillas
" La siguiente línea cambia el tamaño por defecto del tabulador a 3
set tabstop=3
" mantiene 50 líneas de historia de comandos en una sesión vim
set history=50
Y ahora mi parte favorita, los "mapeos" de teclas a comandos.
" Los tres siguientes permite usar el comando externo 'par' que
" viene con casi todas las distribuciones linux (salvo Suse) e incluso
" con cygwin y que permite manipular párrafos de texto
" El siguiente simplemente toma un párrafo (considerando párrafo hasta
" las siguiente línea vacía) y lo ajusta a 78 columnas simplemente pulsando
" F3
map
" El siguiente hace lo mismo pero para un selección hecha en
" modo visual (con el comando v), de ahí la v de 'vmap'
vmap
" Por último, pulsando F4 ajusta el texto a 78 columnas indentando por
" los dos extremos (añadiendo espacios si fuese necesario)
map
" imap hace referencia a comandos en modo 'insertar'. El siguiente
" comando ayuda a escribir textos en LaTex. Si escribes la palabra
" itemize y pulsas (en modo insertar) F4 te crea el begin y end
" correspondientes.
imap
" Y ya que estamos con Latex, aquí tenéis algo cómodo
" F5 guarda el fichero actual y lo compila
map
" F6 invoca al comando xdvi
map
" F7 crea el postscript correspondiente (en compatibilidad PDF) y llama
" al programa "gv"
map
" Por último, F8 crea un pdf y llama al comando xpdf
map
Para finalizar, os hablaré de los pliegues o 'folds'. Son agrupaciones de varias líneas en una única línea que se despliega con un comando. Para más información sobre los pliegues podeís poner (dentro de vim) :help folds.
Yo uso los pliegues cuando escribo un código en C++ o un documento en LaTex muy grande. Para C++, lo que me interesa es que todas las estructuras, clases y subrutinas se compacten. De este modo un código con 6 clases, 14 funciones y la función main, se reduce a la parte de los includes, las variables globables y 21 pliegues, lo cual cabe casi en la ventana de edición por lo que puedo echar un vistazo muy rápido al código completo.
Para manejar los pliegues en un código C++, bastaría con añadir a .vimrc:
map F za
map
El primer mapeo permite conmutar entre abierto y cerrado cuando estamos situados sobre un pliegue pulsado F (en modo comando, se entiende). La segunda línea somplemente crea los pliegues al pulsar shift-F12.
Para LaTex, podríamos hacer, por ejemplo:
map
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Computación
El truco de hoy consiste en lo siguiente. Supongamos que hemos hecho una simulación de un problema en dos dimensiones, o en una pero queremos representar en una figura el espacio (eje x) y el tiempo (eje y). Podemos integrar una rutina en nuestro código (lo cual lo ralentiza) o podemos crear la imagen mediante un software de visualización (por ejemplo MATLAB).
Lo que yo os propongo es más sencillo, utilizar un pequeño script basado en la shell bash y en el potentísimo awk (o gawk) para crearlo.
Así, supongamos que tenemos un fichero con una lista (o matriz) que contiene los dimension_x*dimension_y valores de nuestra figura (por ejemplo en un problema de crecimiento para un sistema 100x100, el fichero sería una lista de 10000 líneas que contienen el valor de la altura en cada uno dos los 100x100 puntos). Se supone que ese fichero lo crea nuestra aplicación.
Una vez que tenemos ese fichero (llamémosle height.dat), creamos un fichero de texto (llamado, p. ej. array2pnm) que contenga la siguiente información
#!/bin/bash
if [ $# -ne 3 ]; then
echo "Sintaxis: $0 Nx Ny fichero_de_entrada "
exit
fi
awk '
BEGIN{max=-100000000; min=100000000;}
{
for (i=1;i<=NF;i=i+1){ if (max<$i) max=$i; if(min>$i) min=$i;
}
}
END{print max,min}' $3 | awk -v Nx=$1 -v Ny=$2 '
BEGIN{print "P2\n#\n\n" Nx,Ny "\n65535"}
NR==1 {
max=$1;
min=$2;
}
{
for(i=1;i<=NF;i=i+1) print int(($i-min)*65535/(max-min)) }' - $3 >$3.pnm
Y lo ejecutamos con la siguiente sintaxis
./array2pnm 100 100 height.dat
Este comando creará el fichero "height.dat.pnm" que se puede visualizar con cualquier programa (por ejemplo display). Si queremos convertirlo a otro formato existen infinidad de librerías. Yo os recomiendo que instaléis el paquete ImageMagick que viene con todas las distribuciones de Linux. Tiene un programa llamado "convert" que hace todo el trabajo.
Por ejemplo
convert height.dat.pnm height.gif
Y ya está...
Publicado por
Unknown
el
miércoles, octubre 11, 2006
1 comentarios
![]()
Etiquetas: Computación

Otro Blog divertido y curioso. Trata sobre la Física en la Ciencia Ficción. Así que su nombre es
Física en la Ciencia Ficción.
EL responsable de éste web imparte una asignatura de libe elección que llama precisamente así, Física en la ciencia ficción, en la Universidad de Oviedo. ¡Quien estudiara asignaturas como ésta!
Adjunto también, por si os interesa, un enlace a la página de Paul Brians, un profesor de la Washington State University, que tiene fichas de libros, con una sección específica de Ciencia Ficción.
Science Fiction-Related Materials
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Ciencia Ficción, Libros
Mirad lo que me he encontrado, je.
Física 1 para ingenieros
Publicado por
Unknown
el
miércoles, octubre 11, 2006
0
comentarios
![]()
Etiquetas: Graciosos
Parece que no abundan los blogs de ciencia, pero éste me ha llamado la atención. Combina magistralmente la divulgación con ciertos toques poéticos.
Esperemos que cada vez haya más blogs de este tipo y que, como el nuestro, resulten útiles y atractivos. ¡Todo por la ciencia!
Publicado por
Mario Castro
el
martes, octubre 10, 2006
0
comentarios
![]()
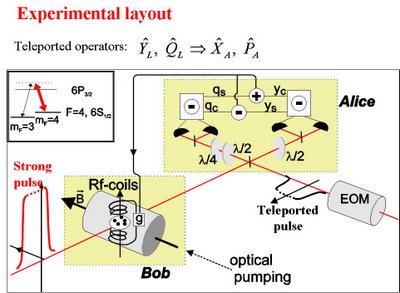
Ahora está de moda lo de la computación cuántica, supongo que porque ya se empiezan a conseguir resultados experimentales. Una de las noticias más recientes es que el grupo del Instituo Niels Bohr, en Copenague, ha conseguido transferir "el estado cuántico de un pulso de luz a una colección de átomos de cesio". No tenía nada claro que quiere decir esto, y he estado buscando la fuente principal para ver si consigo comprenderlo. La aplicación que se busca es la transferir información de un computador cuántico a otro, o de una zona a otra del computador. Sin embargo, lo de que un sistema macroscópico de materia tenga el mismo estado que un haz de fotones, tiene pinta de ser una interpretación de algo más complejo.
Podeis ver la noticia (incluyendo jocosos comentarios sobre la teletransportación) n
Extraído del ABC.
Por supuesto, lo que se ha conseguido es transferir "un" determinado, y no medido, estado cuántico de un haz de fotones a un sistema de átomos de cesio. Se prepara un estado global "entrelazado" y a partir de ahí se trabaja. Intentaré explicarlo mejor cuando tenga un rato para pensarlo. Por ahora os paso una presentación de powerpoint del grupo que ha publicado el artículo:
Presentación sobre el "teletransporte" cuántico>
Y os pongo (¿alguien nos lee?) el enlace al articulillo:
Quantum teleportation between two mesoscopic objects: a photonic pulse and an atomic ensemble
Publicado por
Unknown
el
lunes, octubre 09, 2006
3
comentarios
![]()
Etiquetas: Computación, Cuántica, Física Teórica
Conferencias del planetario
Son del 2 al 30 de noviembre.Todas las conferencias son a las 20 horas.
Jueves, 2 de noviembre, a las 20 horas
Álvaro Giménez Cañete.
Director del Departamento de Investigación y Apoyo Científico, ESA, ESTEC
Europa alrededor de Venus.
La Agencia Europea del Espacio lanzó el año pasado la misión Venus Express a nuestro planeta hermano. En la Semana Santa de 2006 llego a Venus y se inserto en órbita a su alrededor. Después de unos espectaculares descubrimientos iniciales, la nave ha desarrollado un completo programa de investigacion del que se esta obteniendo una nueva visión del planeta. Tan parecido a la Tierra y tan diferente a la vez, Venus esconde la clave para comprender el comportamiento y evolución de las atmósferas planetarias. En la conferencia se presentarán los resultados obtenidos hasta ahora, los programas previstos para los próximos años y el entorno global de la misión en el marco de la exploración del sistema solar de la Agencia Europea del Espacio.
Miercoles, 8 de noviembre, a las 20 horas
Antxon Alberdi Odriozola.
Investigador Científico del CSIC.
Instituto de Astrofísica de Andalucía, IAA.
Viaje al Centro de la Vía Láctea.
El centro de nuestra galaxia es uno de los objetos más brillantes del cielo a diferentes longitudes de onda. En muchos aspectos, recuerda a un núcleo de una galaxia activa de baja luminosidad. En la charla, describiremos la morfología del Centro Galáctico, desde escalas del kiloparsec hasta el parsec central. En el centro dinámico de la galaxia reside un objeto compacto, denominado SgrA*, cuya radiación parece provenir del acrecimiento de materia sobre un agujero negro. Detallaremos las evidencias observacionales, que demuestran la existencia de este agujero negro en el centro de la Vía Láctea, con una masa de unos 2 millones de veces la masa del sol.
Jueves, 26 de noviembre, a las 20 horas.
Rafael Rebolo López.
Profesor de Investigación del CSIC.
Instituto de Astrofísica de Canarias, IAC.
Exoplanetas terrestres.
En la última década se han descubierto unos doscientos planetas alrededor de estrellas parecidas al Sol. Algunos de estos nuevos planetas producen eclipses de sus estrellas, lo que ha permitido en varios casos el estudio detallado de sus principales parámetros físicos. La mayor parte son planetas gigantes gaseosos pero ya se han identificado algunos candidatos a planetas rocosos. El espectacular avance en la investigación de exoplanetas probablemente conducirá a la detección de planetas como la Tierra en la próxima década. Describiremos algunos de los proyectos que podrían conseguir la detección de exoplanetas terrestres en zonas de habitabilidad de estrellas como nuestro Sol. Varios de ellos ya están en marcha.
Jueves, 23 de noviembre, a las 20 horas.
Nicolás Cardiel López.
Profesor Contratado Doctor, Departamento de Astrofísica, Universidad Complutense de Madrid.
La Cosmología o la incesante búsqueda de la belleza.
En la Antártida, los líquenes y comunidades microbianas de los Valles Secos y Montañas Transantárticas no parecen limitados por la más dura combinación de frío, sequedad y radiación que se produce en nuestro planeta. Estas especies son excelentes candidatos para experimentos de exobiología en el espacio exterior, con el fin de demostrar la capacidad de supervivencia de células complejas originadas en la Tierra a posibles transferencias interplanetarias. Los líquenes antárticos han mostrado una extraordinaria resistencia al frío (-196 ºC) y a amplios periodos de frío y sequía (142 meses a -20 ºC) y son capaces de mantener una fotosíntesis activa a temperatura por debajo del punto de congelación. Además, se ha demostrado su capacidad para recuperar altos niveles de fotosíntesis en tan sólo unos minutos después de su exposición a plena luz del sol, tras haber permanecido meses en la oscuridad de la noche polar, cubiertos por una gruesa capa de nieve.
Jueves, 30 de noviembre, a las 20 horas.
José María Bermúdez de Castro Risueño.
Profesor de Investigación del CSIC.
Director del Centro Nacional de Investigación sobre Evolución Humana,
CENIEH, Burgosd.
Atapuerca y su contribución a las investigaciones sobre evolución humana.
Desde el hallazgo en 1976 de la primera mandíbula humana fósil en la Sima de los Huesos las excavaciones sistemáticas e investigaciones de los yacimientos pleistocenos de la Sierra de Atapuerca (Burgos) han dado una ingente cantidad de datos que han permitido dilucidar numerosas cuestiones sobre la evolución biológica y tecnológica de nuestros ancestros. En particular, hemos aprendido mucho sobre la evolución humana en Europa y se han planteado un sinfín de nuevos interrogantes.
TODAS LAS CONFERENCIAS TENDRÁN LUGAR EN LA SALA DE PROYECCIÓN DEL PLANETARIO DE MADRID, QUE TIENE CAPACIDAD LIMITADA.
PARA ACCEDER A LAS MISMAS SERÁ NECESARIO DISPONER DE INVITACIÓN, QUE SE PODRÁ RECOGER, GRATUITAMENTE, EN LA TIENDA DEL PLANETARIO DESDE EL JUEVES ANTERIOR A CADA CONFERENCIA
Publicado por
Unknown
el
miércoles, octubre 04, 2006
0
comentarios
![]()
Etiquetas: Astronomía, Cosmología, Noticias
Anteayer tuve un presentimiento y publiqué una nota sobre la radiación cósmica de fondo. Justo después se publicaron los premios Nobel y, ¡qué increible!, se han dado a físicos que estudiaban la radiación de fondo.
¡¿Soy el único que ve la relación causal?!
Sólo hay dos posibilidades, o mis pensamientos influyeron en la decisión del comité del premio nobel, o fuí capaz de profetizar el resultado. Esto demuestra que:
a) existe la telepatía
b) se puede adivinar el futuro.
No tiene nada que ver un curso de Cosmología que he hecho hace poco...
Ahora en serio, se lo han dado a John C. Mather y a George F. Smoot por el descubrimiento de la forma del cuerpo negro y la anisotropía de la radiación cósmica de microondas de fondo. Esta anisotropía permite explicar el origen de las galaxias, como se puede ver en el enlace correspondinte al COBE que di profeticamente.
Para más información consulten éste mismo BLOG (léase bilog si fuese idiota) o bien
Los que más saben de cosmología
Publicado por
Unknown
el
miércoles, octubre 04, 2006
0
comentarios
![]()
Etiquetas: Física General, Graciosos, Noticias
Como todo el mundo sabe mucho de lo que se desarrolla ahora mismo en Cosmología tiene que ver con los datos aportados por el COBE. Este satélite dispone de varios sistemas para medir la radiación del fondo cósmico.
En estas imágenes podemos ver algunos resultados interesantes del COBE. En la primera imagen se ve que la radiación es prácticamente homogénea y se corresponde perfectamente con la radiación de un cuerpo negro a 2,728K. Esto último no se deduce de esta imagen, evidentemente, sino de otro dispositivo colocado en el COBE, que compara el espectro de un cuerpo negro con el de la radiación, el Far Infrared Absolute Spectrophotometer (FIRAS)
La segunda imagen da una idea de como es el diposlo. Aquí se exageran las diferencias de temperatura, haciendo que sean visibles diferencias de mK. La zona hacia la que se acerca la Tierra (arrastrada por el movimiento de toda la galaxia) sufre un pequeño corrimiento hacia el azul, y la arte opuesta hacia el rojo. Esto permite definir una especie de Éter, un sistema de referencia bastante "absoluto". aunque no es así, evidentemente. Se trata de coger la referencia de un sistema respecto al cual la radiación de fondo es homogénea.
La tercera imagen presenta diferencias de microKelvin, restando el dipolo. Aquí podemos observar la galaxia, y vemos irregularidades que se explican únicamente mediante el modelo inflaccionario.
Si quereis ver un curso de cosmología:
Curso de Cosmología
Y el resto de datos sobre el COBE en
COBE
Publicado por
Unknown
el
lunes, octubre 02, 2006
0
comentarios
![]()
Etiquetas: Cosmología, Física Teórica
Un amigo me contó que existía este artículo:
http://pauli.uni-muenster.de/~munsteg/arnold.html
Del que extraigo un par de "extractos":
"Mathematics is a part of physics. Physics is an experimental science, a part of natural science. Mathematics is the part of physics where experiments are cheap."
algo así como: "Las matemáticas son una parte de la Física. La Física es una ciencia experimental, es decir, parte de la ciencia de la naturaleza. Las Matemáticas son la parte de la Física en la que hacer experimentos es barato"
Seguimos:
"In the middle of the twentieth century it was attempted to divide physics and mathematics. The consequences turned out to be catastrophic. Whole generations of mathematicians grew up without knowing half of their science and, of course, in total ignorance of any other sciences."
" A Mitad del siglo veinte se intentó dividir la física y la matemática. Las consecuencias fueron catastróficas. Generaciones de matemáticos crecieron conociendo la mitad de la ciencia y, por supesto, con total ignorancia del resto de ciencias."
¿Qué os parece? Bastante atrevido. Está claro que la Física se estudia al mismo tiempo que las matemáticas, y que la intuición física ayuda a comprender mejor esas matemáticas. intentad enseñarle a alguien ecuaciones diferenciales de manera abstracta y luego contadle que cierta ecuación es la que describe un muelle y por eso la solución es un seno "amortiguado" o que esta otra describe movimientos planetarios. es bastante más sencillo. De hecho, ¿tiene sentido estudiar ecuaciones diferenciales si no se aplicasen a lo que observamos en la naturaleza?
On teaching mathematics by V.I. Arnold
This is an extended text of the address at the discussion on teaching of mathematics in Palais de Découverte in Paris on 7 March 1997.
Mathematics is a part of physics. Physics is an experimental science, a part of natural science. Mathematics is the part of physics where experiments are cheap.
The Jacobi identity (which forces the heights of a triangle to cross at one point) is an experimental fact in the same way as that the Earth is round (that is, homeomorphic to a ball). But it can be discovered with less expense.
In the middle of the twentieth century it was attempted to divide physics and mathematics. The consequences turned out to be catastrophic. Whole generations of mathematicians grew up without knowing half of their science and, of course, in total ignorance of any other sciences. They first began teaching their ugly scholastic pseudo-mathematics to their students, then to schoolchildren (forgetting Hardy's warning that ugly mathematics has no permanent place under the Sun).
Since scholastic mathematics that is cut off from physics is fit neither for teaching nor for application in any other science, the result was the universal hate towards mathematicians - both on the part of the poor schoolchildren (some of whom in the meantime became ministers) and of the users.
The ugly building, built by undereducated mathematicians who were exhausted by their inferiority complex and who were unable to make themselves familiar with physics, reminds one of the rigorous axiomatic theory of odd numbers. Obviously, it is possible to create such a theory and make pupils admire the perfection and internal consistency of the resulting structure (in which, for example, the sum of an odd number of terms and the product of any number of factors are defined). From this sectarian point of view, even numbers could either be declared a heresy or, with passage of time, be introduced into the theory supplemented with a few "ideal" objects (in order to comply with the needs of physics and the real world).
Unfortunately, it was an ugly twisted construction of mathematics like the one above which predominated in the teaching of mathematics for decades. Having originated in France, this pervertedness quickly spread to teaching of foundations of mathematics, first to university students, then to school pupils of all lines (first in France, then in other countries, including Russia).
To the question "what is 2 + 3" a French primary school pupil replied: "3 + 2, since addition is commutative". He did not know what the sum was equal to and could not even understand what he was asked about!
Another French pupil (quite rational, in my opinion) defined mathematics as follows: "there is a square, but that still has to be proved".
Judging by my teaching experience in France, the university students' idea of mathematics (even of those taught mathematics at the École Normale Supérieure - I feel sorry most of all for these obviously intelligent but deformed kids) is as poor as that of this pupil.
For example, these students have never seen a paraboloid and a question on the form of the surface given by the equation xy = z^2 puts the mathematicians studying at ENS into a stupor. Drawing a curve given by parametric equations (like x = t^3 - 3t, y = t^4 - 2t^2) on a plane is a totally impossible problem for students (and, probably, even for most French professors of mathematics).
Beginning with l'Hospital's first textbook on calculus ("calculus for understanding of curved lines") and roughly until Goursat's textbook, the ability to solve such problems was considered to be (along with the knowledge of the times table) a necessary part of the craft of every mathematician.
[...]
V.I. Arnold
Publicado por
Unknown
el
lunes, octubre 02, 2006
0
comentarios
![]()
Etiquetas: Artículos, Física General, Matemáticas, Noticias