Qué puedo hacer con ordenador cuántico que no pueda hacer con mi PC

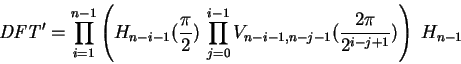
Muy buena pregunta. ¿Qué se puede hacer con qbits que no se pueda hacer con bits? En realidad se puede hacer lo mismo,según dijo Cirac en una conferencia. La diferencia está en cómo se hacen las cosas.
Pondré algunos ejemplos, porque no soy un experto en computación cuántica, por desgracia. En criptografía se usan algoritmos cuya fortaleza está basada en que para desencriptar un texto encriptado sin conocer las claves correspondientes, es necesario factorizar un número en factores primos. Es el caso del sistema de clave pública/clave privada como el RSA, el tiempo que se tarda en hacerlo es demasiado grande. Éste tiempo depende exponencialmente del tamaño de la clave.
Sin embargo, si se usase un computador cuántico, podríamos usar el algoritmo de Peter Shor, científico de la AT&T, que permite factorizar un número muy grande en tiempo polinómico. Lo hace usando una transformada de Fourier cuántica.
Podéis ver el algoritmo de factorización mediante computación cuántica en el enlace, y os recomiendo este documento: Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer.
Si tenemos un sistema 2ⁿ, si usamos una transformada de Fourier clásica, necesitaremos n*2ⁿ pasos, mientras que si usamos una transformada de Fourier cuántica, como la diseñada por Ekert y Sozsa en 1996(Approximate Quantum Fourier Transform and Decoherence), solamente necesitamos n² pasos, algo mucho más manejable sin duda.
El tamaño de la clave no influye, se puede resolver casi en el mismo tiempo una clave de 2048 bits que una actualmente más potente de 8000. Ahora ya no es el exponente, es una base. Pero la computación cuántica no solamente rompe la clave RSA calculando la factorización, usando los algoritmos adecuados, puede bucar claves simétricas, resolver problemas N=NP y realizar cálculos estadísticos, que podrían darnos otros avances en la criptografía.